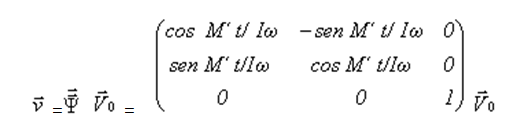I – Antecedents.

According to Galileo’s Relativity Principle, laws in physics are identical in any inertial reference system. The Classical Mechanics, and even most of the modern theories in physics, have been formulated for inertial reference frames, checking their validity in this type of systems.

Nevertheless, out of these limits there are other assumptions in nature, for which we nowadays still ignore the laws of their behaviour. One example is the analysis of rigid bodies equipped with rotational movement, because in their case it is necessary to take into account inertial reactions which might happen. From a relativistic point of view, an intrinsic rotation can be seen as a fixed mobile and a rotation of the space of events which contains it. In this assumption, different experiments can be carried out, and the resulting observations be noted. By way of illustration we could propose:

 1. Multiple rotations. A rigid mobile exposed to successive non coaxial torques might react with two simultaneous non coaxial rotations. In this assumption, the coordinate system defined by one position vector and the Euler angles for indicating its orientation, does not adequately identify the evolution of the position of each point of the mobile in a bi-univocal manner. A new reference system, adequate for these assumptions, is thus necessary.

2. Gyroscopic moment. In the assumption of a body equipped with intrinsic rotation, the action of a new non-coaxial moment generates an inertial reaction named gyroscopic moment, which does not correspond to the laws of Newton, and which finds itself unstructured within classical mechanics. It is therefore necessary to include this phenomenon, and in general the inertial interactions, in a logical and scientific structure, within the scope of the mechanics.

These experimental references, as well as many others which might be proposed, infer the existence of a different rotational dynamics, non-Newtonian, necessary for the identification of the behaviour of rotating bodies, when exposed to new non-coaxial stimulations, and the behaviour of which, in many cases, nowadays is considered to be anomalous, paradoxical or chaotic, because the laws that we have at our disposal do not allow to identify and predetermine it.

 

II- Deduction.

This new non inertial and non-Newtonian rotational dynamics can be at least inferred in two differentiated ways:

• Relativistic deduction.
• Non relativistic deduction.

 

Relativistic deduction. Using an abstract method, one can mathematically infer a system of equations, which allow the comprehension of the fundamental interactions generated in nature. These equations show how the matrix of a tetra-dimensional rotation of a reference frame is associated with the inertial field Tⁱ_jk originated by the rotation, and new motion equations can be deduced, hence a general expression of the motion equations in the gravitation theory of Einstein.

 

Non relativistic deduction. In the assumptions of simultaneous non coaxial rotations the rigid body experiences non homogeneous speed fields. Said fields with non homogeneous distributions, generate anisotropic acceleration fields. These fields can be interpreted as fields of inertial forces, created in space through the effect of simultaneous non coaxial rotations.

Based on the expressed, we can interpret that the gyroscopic momentum does not physically exist, as it simply is the observable effect of a field of inertial forces generated by simultaneous, non-coaxial, rotation of space. This phenomenon might get structured in a new non inertial rotational dynamics, within the scope of the Theory of Dynamic Interactions.

Nevertheless, the mentioned gyroscopic momentum has been quantified, through multiple procedures of the classical mechanics, with the following formulation:

D = I Ω ω       (1)

 

Based on the Principle of Conservation of the Momentum, this torque will be equivalent to the one acting from the outside. Therefore we can infer that the field of inertial forces generated in the rotating space by a new non coaxial momentum M´, upon a moving body with a rotational movement  and an inertial momentum I upon that rotation axis, and thus with an angular momentum , will oblige the moving body to acquire a precession rate , defined by the scalar ratio:

 Ω = M´/ (I ω) = M´/ L       (2)

 

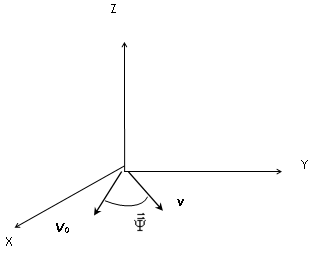
Figure 1.The rotational operator  transforms, through one rotation, the speed vector into the vector v, both always situated on an identical plane, in this  example in the plane XY.

 

This precession rate  can be observed simultaneously to the initial , which stays constant within the body. In a first approach we will consider it as instantaneous with the action of the momentum M´. Further, and as discriminating hypothesis, in the case of transfer movement of the body, we propose the dynamic hypothesis of the transfer speed field coupling to the anisotropic field of inertial speeds created by the second non-coaxial momentum, obtaining as resultant movement a simultaneous orbiting with the intrinsic rotation of the moving body. This new orbiting movement, generated by a non-coaxial momentum, defines itself through the rotation of the speed vector, the latter being kept constant in module.

In the assumption of figure 1, the new external momentum M´, which is supposed to be located on the X-axis, will generate an inertial rotation around the Z-axis, and if the transfer vector  was located on the XY plane, also the resulting speed after the rotation will stay on that plane. Therefore, the space rotation matrix  will be as follows:

 

And it will, in our assumption, generate a rotation of the referred transfer vector   in the plane XY. As motion equation we obtain:

          (3)

But, as:

α =  Ω.t         (4)

and, according to equation (2):

 α = M´. t/ (I ω)        (5)

the motion equation ends up as follows:

       (6)

So we can associate dynamic effects to speed, and a clear mathematical correlation between rotation and transfer. This mathematical correlation allows us to identify a physical relation between transfers of kinetic rotational energy to kinetic transfer energy, and vice-versa.

Quite a number of examples can be thought of for checking these dynamic hypotheses, which would allow us to interpret many assumptions in nature, which still remain unexplained.

This new non-inertial rotational dynamics based on the Theory of Dynamic Interactions, is developed in laws and corollaries, allowing a number of new, unknown scientific and technological applications.

 

III – Generalization of the mechanics.

As we expressed in the beginning, the classical mechanics has been formulated for inertial reference frames, and not for rotating spaces of events. Nevertheless, it is possible to think of a new mechanics for any type of space, adding their inertial reactions and defining a dynamics of inertial fields. Thus, the inertial phenomena would also be structured, and get incorporated in a unified mechanics.

In order to incorporate the inertial phenomena into the structure of physical knowledge, it is necessary to analyze the motion in non-holonomous coordinates and the resulting axial reactions, in the understanding that a mechanics, as the classical mechanics, based on holonomous coordinates and polar reactions, will only represent a limited and partial view of nature.

The proposed generalization does not say that classical mechanics is obsolete or wrong, but simply that it is partial and limited, as it refers to the specific assumption of inertial systems. We wish and are able to be more ambitious, looking for more general dynamic laws, which establish the behaviour of moving bodies when rotating, or even when they are exposed to multiple non-coaxial rotations of the space of events.

The Theory of Dynamic Interactions generalizes the concept of gyroscopic momentum, and of other inertial phenomena, incorporating them into the unified structure of a new non inertial rotational dynamics.

According to the defended Theory of Dynamic Interactions, we can conceive a universe in a constant dynamic balance, in which a force momentum, with a zero resultant, will generate, as long as it works, a movement of constant orbiting, within a closed path. The importance of this mathematical model is obvious, in which not only the forces are leading players, but also the momentums of forces which, while staying constant, will generate orbiting and constantly recurrent movements, generating a system in dynamic balance, and not in unlimited expansion. This Theory of Dynamic Interactions is reasoned out and described in the new book of Gabriel Barceló: Un Mundo en Rotación (2008), and its antecedents and fundamentals were presented in the book of the same author: El Vuelo del Bumerán (2005).

 

IV – Celestial mechanics.

The deductions arising from this rotational dynamics may prove relevant in resolving the dynamic problems related to the cosmos. Normal and repeated movements of celestial bodies in the universe are accelerated by rotation, except for free-falling ones. Nevertheless, Einstein’s general theory of relativity, special relativity, Galileo-Newtonian relativity and, classical mechanics in general are based on the principle of translational relativity. These theories consider transformations in translational holonomic coordinates, consequently, when they describe rotational movements, the angular coordinate transformations must be added to the translational coordinate transformations. The Theory of Dynamic Interactions enables a truer and simpler identification of constantly rotating and orbiting celestial bodies.

There is still plenty of room left in the standard cosmological model for extensive work on relativist mechanics by applying a theory of rotational relativity, which would make it possible to better understand the behaviour of the universe.

When observing dynamic systems in which simultaneous intrinsic rotational and orbiting movements are observed, the existence of dynamic interactions can be inferred.

In addition to enabling us to better understand the universe, the Theory of Dynamic Interactions enables us to conceive of a real galactic dynamics and explain the why of the ecliptic plane and the wherefore of Saturn’s rings. Accordingly, we deduce that the rings generated in planetary systems may be the result of the action of a constant, external couple within the framework of this theory.

The theory enables us to resolve a puzzle: confirm and understand the physical and mathematical correlation between orbiting and intrinsic rotation and, consequently, the reason why we have night and day on the Earth, given that this theory points to a clear correlation between the intrinsic rotation of the Earth and its orbital path. 

The theory defines a model universe in which forces do not always create accelerations in proportion to mass, which would imply infinitely increasing speeds for a constant force. Instead, the force momenta produce a dynamic equilibrium on transferring the linear speeds to orbital speeds and transforming the rectilinear paths into curving and orbiting ones, whereas in classical mechanics, and in accordance with Newton’s second law, dynamic causes are associated with changes of speed.

The publisher, Editorial Arpegio SL, has just published a two-volume, treatise by Gabriel Barceló on the evolution of the knowledge of our environment: Imago Universi: Una concepción humana del cosmos. It is a treatise on cosmology, the last chapter of which deals in suggestions on the application of the Theory of Dynamic Interactions (TDI) to dynamic forces in the universe. A video presentation of the book has been made (See video), which is also the subject of a website (Go to website).

It the last chapter of Imago Universi, this theory is put forward as a new conceptual structure within which to examine dynamics in non-inertial frameworks and, particularly, the celestial dynamics of rigid bodies subject to numerous, non-coaxial rotations. Some time after, and to serve as a summary of the Imago Universi treatise, the International Journal of Astronomy and Astrophysics published the article entitled “Proposal of New Criteria for Celestial Mechanics” by the same author (See article), in which an approach to the application of the Theory of Dynamic Interactions is analysed to better understand our cosmological setting and celestial mechanics.